En 1822 paraît la Théorie analytique de la chaleur par le mathématicien Joseph Fourier. Bien que l’auteur ait publié les premiers résultats de ses travaux dès 1807, ce livre en présente une synthèse qui aura une postérité exceptionnelle dans la science contemporaine, contredisant sans nul doute cette allusion de Victor Hugo : “Il y avait à l’académie des sciences un Fourier célèbre que la postérité a oublié et dans je ne sais quel grenier un Fourier obscur dont l’avenir se souviendra.” [1]Victor Hugo, Les Misérables, Livre Troisième, 1890 En effet, peut-être se souvient-on de l’influence du philosophe Charles Fourier sur le socialisme du XIXe siècle, mais ce qui est certain c’est que les idées du mathématicien Joseph Fourier ont eu un écho considérable dans les sciences de ces deux derniers siècles et qu’elles sont encore utilisées aujourd’hui par des milliers de scientifiques et d’ingénieurs à travers le monde.

Joseph Fourier (par Julien-Léopold Boilly, domaine public)
De quoi est-il question dans la Théorie analytique de la chaleur ? Ce qui en fait un ouvrage exceptionnel, ce n’est pas tant par le contenu traitant de la manière dont la chaleur se propage dans les objets (dont un exemple contemporain serait l’isolation thermique des bâtiments), mais bien par la méthode employée et les outils mathématiques d’une portée très générale qui y sont développés. À cette époque on parle d’ailleurs de physique-mathématique pour qualifier cette branche des sciences naturelles qui s’attache à décrire la réalité du monde par les lois mathématiques, à la suite des Principia Mathematica de Newton.
Le Discours préliminaire de l’ouvrage de Fourier est particulièrement éclairant sur la démarche des physiciens de l’époque. En voici le tout premier paragraphe :
« Les causes primordiales ne nous sont point connues ; mais elles sont assujetties à des lois simples et constantes, que l’on peut découvrir par l’observation, et dont l’étude est l’objet de la philosophie naturelle ». [2]J. Fourier, Théorie analytique de la chaleur, Firmin Didot, 1822. Texte complet sur https://fr.wikisource.org/wiki/Th%C3%A9orie_analytique_de_la_chaleur/Discours_pr%C3%A9liminaire
Dans ces quelques lignes se trouvent le programme de la science moderne : les phénomènes sont un enchaînement de causes et de conséquences qui sont la manifestation de lois. Ces lois sont simples, c’est-à-dire que l’on peut les exprimer de manière univoque et concise, souvent par une équation mathématique. Elles sont constantes, c’est-à-dire qu’elles sont les mêmes partout dans l’espace (ce qu’avait compris Newton) et inchangées depuis la nuit des temps. Elles sont déduites de l’observation, et non plus de principes philosophiques ou théologiques comme c’était le cas depuis l’antiquité. Fourier est conscient que la mathématisation du monde, que l’on nomme ici analyse, donnera une fécondité inouïe aux sciences naturelles. Mais de surcroit il s’agit d’un outil donné à l’esprit humain pour comprendre, et on pourrait dire contempler le cosmos, comme on le ressent à la lecture de ces lignes :
« Si la matière nous échappe comme celle de l’air et de la lumière par son extrême ténuité, si les corps sont placés loin de nous, dans l’immensité de l’espace, si l’homme veut connaître le spectacle des cieux pour des époques successives que sépare un grand nombre de siècles, si les actions de la gravité et de la chaleur s’exercent dans l’intérieur du globe solide à des profondeurs qui seront toujours inaccessibles, l’analyse mathématique peut encore saisir les lois de ces phénomènes. Elle nous les rend présents et mesurables, et semble être une faculté de la raison humaine destinée à suppléer à la brièveté de la vie et à l’imperfection des sens ; et ce qui est plus remarquable encore, elle suit la même marche dans l’étude de tous les phénomènes ; elle les interprète par le même langage, comme pour attester l’unité et la simplicité du plan de l’univers, et rendre encore plus manifeste cet ordre immuable qui préside à toutes les causes naturelles ». [3]Ibid
Venons-en maintenant au contenu de l’ouvrage. Plus loin dans le Discours préliminaire, Fourier écrit, parlant des mouvements de la chaleur :
« […] si l’ordre qui s’établit dans ces phénomènes pouvait être saisi par nos sens, ils nous causeraient une impression comparable à celles des résonances harmoniques ». [4]Ibid
Comment comprendre cette phrase et que sont les “résonances harmoniques” ? Fourier fait référence ici au phénomène de la corde vibrante, c’est-à-dire aux différents sons que peut produire une corde livrée à elle-même dans son mouvement oscillant comme peut l’être une corde de guitare, de piano, ou encore un pizzicato de violon. On peut observer sur une guitare par exemple que le mouvement de la corde est généralement plus important en son centre. Cette partie ample du mouvement est appelée ventre et les extrémités de la corde qui sont fixes sont appelées nœuds. Mais il est aussi possible avec une certaine technique de faire sonner la corde une octave au-dessus, et dans ce cas le centre de la corde devient aussi un nœud avec deux ventres de part et d’autre. Ce problème était déjà bien étudié à l’époque de Fourier. L’équation mathématique du mouvement (la loi au sens que nous venons de voir) était connue et on savait que les fonctions trigonométriques (sinus et cosinus), que l’on pourrait appeler dans ce contexte des ondes pures, sont des solutions particulières du problème sous réserve de contraindre leur période à une suite de nombres bien spécifique (voir la figure ci-dessous). L’onde qui se manifeste par un ventre unique au milieu de la corde est appelée fondamentale, tandis que les autres de période plus courte sont les harmoniques. La période d’une harmonique est nécessairement une division entière de la fondamentale, par exemple ½ pour l’octave, ⅓ pour une octave plus une quinte, etc. Aucune autre période n’est admise : c’est la résonance.
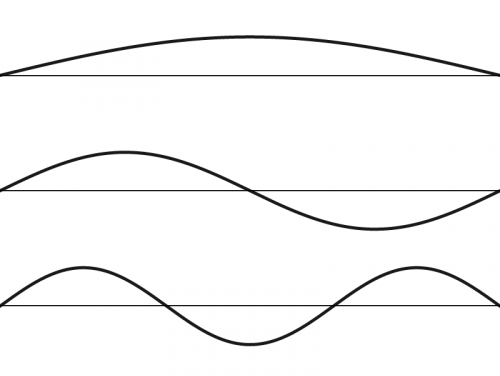
Trois premiers modes de la corde vibrante, de haut en bas : fondamentale, première harmonique et seconde harmonique.
Ce qui était aussi connu à l’époque c’est qu’une somme de ces ondes pures admissibles est aussi une solution admissible du mouvement de la corde. Il est ainsi possible, en modulant le poids des différentes harmoniques de parvenir à des profils de corde très différents pour une même note fondamentale. C’est ce qui explique, avec l’attaque (premiers instants du son), la différence de timbre des instruments de musique.
Quel rapport avec la propagation de la chaleur ? Dans un premier temps, Fourier réalise que la loi fondamentale du mouvement de la chaleur qu’il a obtenue par l’observation impose un certain nombre de propriétés communes entre l’évolution des profils de températures et la forme des cordes vibrantes, d’où sa remarque que nous venons de citer. Mais Fourier ne s’arrête pas là car pour lui l’objet des sciences n’est pas seulement de trouver les lois de la nature mais aussi de pouvoir établir des prédictions. À partir d’une situation de départ, on doit pouvoir calculer numériquement pour n’importe quel instant du futur la valeur des températures, ou la position de la corde dans l’exemple que nous venons de décrire. Or pour ces deux problèmes, seules les situations initiales d’ondes pures se prêtent à ce calcul, ce qui est beaucoup trop restrictif. Évoquant le résultat numérique, Fourier écrit :
« On peut dire que tant qu’on ne l’a pas obtenu, les solutions demeurent incomplètes ou inutiles, et que la vérité qu’on se proposait de découvrir n’est pas moins cachée dans les formules d’analyse, qu’elle ne l’était dans la question physique elle-même ». [5]Ibid
C’est donc pour obtenir les résultats numériques dans toutes les situations que Fourier réalise un véritable tour de force qui lui vaudra la postérité : il trouve la formule mathématique permettant de décomposer n’importe quel profil en somme d’ondes pures, autrement dit la formule qui permet de calculer les poids des différentes harmoniques. On peut dire d’une certaine manière que Fourier a élaboré un outil conceptuel analogue au prisme optique de Newton : le prisme fait jaillir les couleurs de l’arc-en-ciel à partir de la lumière blanche qui y entre. La formule de Fourier révèle les ondes pures qui se cache dans les formes les plus arbitraires. Calculer l’évolution d’un profil de température ou d’une corde vibrante revient à décomposer l’instant initial en ondes pures pour lesquelles l’évolution est aisée à calculer, puis à sommer l’ensemble de ces ondes. C’est ce qu’on appelle l’analyse harmonique.
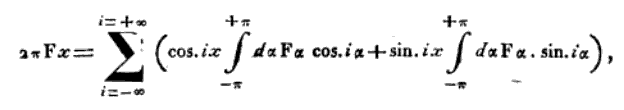
La formule de Fourier dans la gravure de 1822. Voici comment on peut la lire : Deux fois le nombre π (pi) fois la fonction F (forme que l’on veut décomposer) de la variable x égale la somme (symbole Σ) pour i (numéro de l’harmonique) allant de moins l’infini à plus l’infini de cosinus i x (onde pure de mode i) fois l’intégrale (symbole ∫) selon α (alpha) de moins π à plus π de F de α fois cosinus i α, plus la même chose pour l’onde sinus i x. Les intégrales (ce qui est à droite du symbole ∫) permettent de calculer le poids des différentes harmoniques, on les nomme aujourd’hui coefficients de Fourier.
On imagine sans peine la grande fécondité ultérieure d’un résultat à la fois si fondamental et d’une telle généralité. Ce fut le cas et jusqu’à aujourd’hui dans tous les domaines de la physique, mais également dans d’autres branches des mathématiques comme les probabilités, les algorithmes et la science des données, l’imagerie médicale, etc.
Si l’on se borne à l’étude de la chaleur, le travail de Fourier a eu un impact important sur la compréhension du climat et de l’effet de serre en particulier, même s’il faudra attendre la fin du XIXe et le début du XXe siècle pour comprendre la nature du rayonnement thermique que Fourier appelle chaleur lumineuse lorsqu’elle provient du soleil et chaleur obscure lorsqu’elle vient du sol et des objets. Il donnera également une formule pour calculer l’âge de la terre en se basant sur les observations de la variation des températures souterraines en fonction de la profondeur. Sans doute par prudence il n’avancera pas de résultat numérique précis (il évoque “une très longue suite de siècles” [6]J. Fourier, Refroidissement séculaire du globe terrestre, Bulletin des Sciences par la Société philomathique de Paris, 1820 ) et 40 ans plus tard Lord Kelvin en Angleterre reprendra le raisonnement conduisant à la perspective abyssale de plusieurs dizaines millions d’années. Le calcul est erroné (la valeur admise aujourd’hui est de 4,5 milliards d’années) car il ne prend pas en compte les mouvements de convection du manteau terrestre, apportant l’énergie thermique des profondeurs du globe jusqu’aux couches superficielles, phénomène inconnu à l’époque. Mais la démarche force le respect. En tout cas elle est l’illustration des ambitions de Fourier : utiliser les mathématiques pour rendre accessibles à l’humanité les échelles de temps géologiques, et ainsi “suppléer à la brièveté de la vie et à l’imperfection des sens”.
Lorsque son œuvre maitresse est publiée en 1822, Fourier est au sommet de sa carrière. Il est membre de l’Académie des Sciences depuis 1817 et sera reçu à la Royal Society de Londres en 1823 et élu à l’Académie française en 1826. Mais loin de l’image d’Épinal du savant solitaire enfermé dans son laboratoire, Joseph Fourier fut pleinement engagé dans son époque marquée par une incroyable effervescence intellectuelle et les tragédies des guerres de la Révolution et de l’Empire. Il occupa une place primordiale dans l’expédition scientifique qui accompagna Bonaparte en Egypte entre 1798 et 1801, et il écrira la préface du monumental compte-rendu Description de l’Égypte. Durant sa carrière, il dut partager son temps entre sa recherche, ses étudiants (il fut professeur à l’École Polytechnique et à l’École Normale Supérieure), ses tâches administratives (il fonde la Faculté des Sciences Grenoble et en devient le recteur) et ses responsabilités politiques (il est préfet de l’Isère de 1802 à 1815 puis préfet du Rhône en 1815). Après la disparition de Fourier en 1830, François Arago conclura son hommage à l’Académie des Sciences par ces mots :
« Mon but aura été complètement atteint, si, malgré l’imperfection de mes esquisses, chacun de vous a compris que les progrès de la physique générale, de la physique terrestre, de la géologie, multiplieront de jour en jour davantage les fécondes applications de la Théorie analytique de la chaleur, et que cet ouvrage portera le nom de Fourier jusqu’à la postérité la plus reculée ». [7]F. Arago, Éloge historique de Joseph Fourier, séance publique du 18 novembre 1833. Le texte est riche de détails et d’anecdotes sur la vie du mathématicien, il est disponible ici : … Continue reading
References
| ↑1 | Victor Hugo, Les Misérables, Livre Troisième, 1890 |
|---|---|
| ↑2 | J. Fourier, Théorie analytique de la chaleur, Firmin Didot, 1822. Texte complet sur https://fr.wikisource.org/wiki/Th%C3%A9orie_analytique_de_la_chaleur/Discours_pr%C3%A9liminaire |
| ↑3 | Ibid |
| ↑4, ↑5 | Ibid |
| ↑6 | J. Fourier, Refroidissement séculaire du globe terrestre, Bulletin des Sciences par la Société philomathique de Paris, 1820 |
| ↑7 | F. Arago, Éloge historique de Joseph Fourier, séance publique du 18 novembre 1833. Le texte est riche de détails et d’anecdotes sur la vie du mathématicien, il est disponible ici : https://www.academie-sciences.fr/pdf/dossiers/Fourier/Fourier_pdf/Fourier_Arago.pdf |